여러분 제가 백준 점수 버그를 발견했습니다 이 코드를 다른곳에 5번 옮기고 제출을 누르면…
국내의 알고리즘 문제 풀이 서비스를 제공하는 웹 사이트인 백준 온라인 저지가 있습니다.
그리고 그 백준 온라인 저지에 있는 문제들의 난이도를 매기고, 그 난이도를 기반으로 유저들에게 티어를 부여해주는 웹 사이트 Solved.ac이 있습니다.
많은 유저들이 Solved.ac의 티어를 올리고, 이 티어를 바탕으로 많이 이야기하곤 합니다. 그래서 유저들은 티어 레이팅을 많이 주는 문제를 풀고, 빨리 티어를 올리기를 원합니다.
이 게시글에서는 알고 있으면 빠르게 티어를 올리는 데에 유리한 알고리즘중 하나인 세그먼트 트리에 대해서 알아보겠습니다.
1. 세그먼트 트리란?
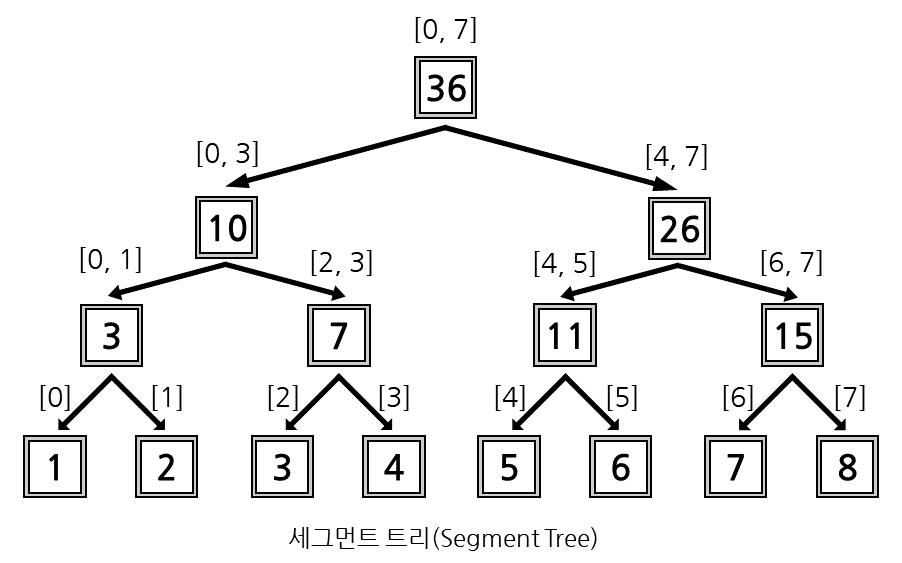
세그먼트 트리(Segment Tree)는 자료구조의 일종으로, 이름에서 알 수 있듯, 트리 형태의 자료 구조입니다. 정확히는 완전 이진 트리로 구성된 자료구조중 하나입니다.
세그먼트 트리는 다음과 같은 특징을 가지고 있습니다.
- 세그먼트 트리는 여러개의 데이터에 대한 정보를 트리에 저장하여 이용합니다.
- 세그먼트 트리의 리프 노드에는 여러개의 데이터에 해당하는 값이 저장되어 있습니다.
- 부모노드는 자식 노드 구간에 대한 데이터를 가지고 있습니다.
- 특정 구간 내의 데이터에 대한 처리(구간 합, 구간 곱 등…)와 특정 데이터 변경을 $O(\log N)$의 시간 복잡도로 해결 가능합니다.
위 그림은 데이터 1, 2, 3, 4, 5, 6, 7, 8에 대한 세그먼트 트리이고, 각 구간은 자식 노드의 합을 가지고 있습니다!
2. 구현
세그먼트 트리는 생성, 계산, 갱신으로 이루어져 있습니다.
이하 예시들은 위 그림과 같은 합 세그먼트 트리를 바탕으로 구현했습니다.
2.1. 기초
1
2
3
4
#define MAX_ARRAY_SIZE 1000001
#define MAX_TREE_SIZE MAX_ARRAY_SIZE * 4
int segTree[MAX_TREE_SIZE];
int arr[MAX_ARRAY_SIZE];
우선 입력할 데이터와 세그먼트 트리에 사용되는 배열을 전역 변수로 선언합니다. 모든 계산은 함수로 구현될것이기 때문에 전역변수로 처리하는것이 속도, 공간, 코드 가독성상 이득입니다.
그리고, 배열의 최대값을 MAX_ARRAY_SIZE로 지정하고, 세그먼트 트리의 최대 사이즈를 MAX_ARRAY_SIZE의 4배로 지정합니다. 그 이유는 다음과 같습니다.
- 리프 노드의 개수는 입력될 데이터 개수와 같습니다.
- 리프 노드가 $N$개인 완전 이진트리의 높이 $H$는 $\lceil \log N \rceil$입니다.
- 높이가 $H$인 완전 이진트리의 최대 노드 개수는 $2^{H+1}-1$입니다.
- 입력될 데이터 개수가 $N$개인 세그먼트 트리는 $N$과 $\frac{2^{\lceil \log N \rceil +1}-1}{N}$배 차이납니다.
- 그래프를 통해 $\frac{2^{\lceil \log N \rceil +1}-1}{N}$가 4가 최대값임을 알 수 있습니다.
위와 같은 이유로 Naive하게 세그먼트 트리 노드의 크기는 4배로 지정해주면 Outofbounds 에러를 마주칠 일은 없을겁니다.
2.2. 생성
1
2
3
4
5
6
int init(int node, int start, int end){
if(start == end)
return segTree(node] = arr[start];
int mid = (start + end)/2;
return segTree[node] = init(node*2, start, mid) + init(node*2+1, mid+1, end);
}
입력한 데이터인 arr배열을 세그먼트 트리로 바꿔주는 함수입니다. init(1, 0, N-1) 형태로 사용합니다.
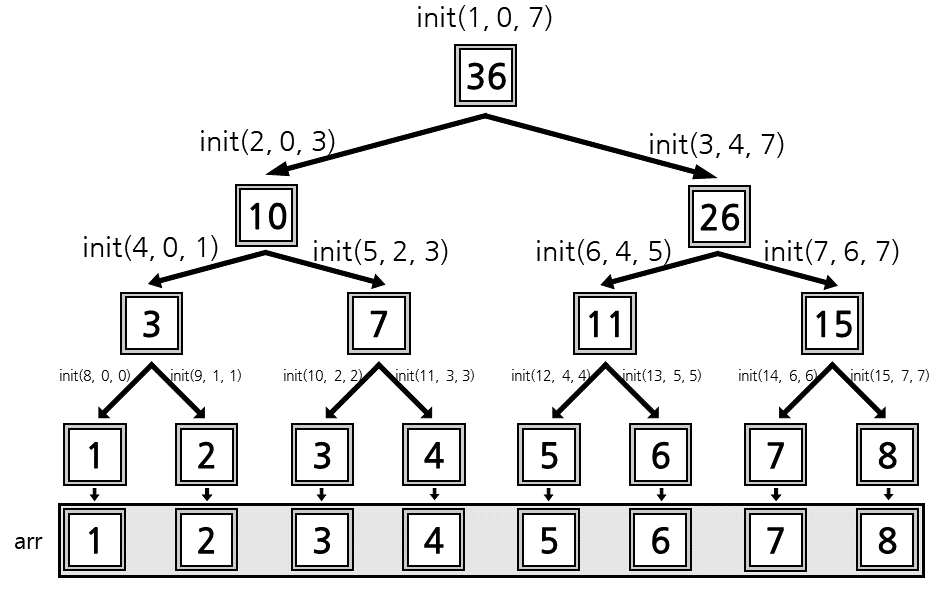
첫번째 매개변수인 node는 세그먼트 트리 배열에 할당될 노드의 인덱스를 의미합니다. 가장 위 root노드의 인덱스는 1이고, 자식 노드가 있는 노드의 인덱스가 node이라고 하면 왼쪽 자식은 2*node, 오른쪽 자식은 2*node+1로 불러 올 수 있습니다.
두번째와 세번째 매개변수인 start와 end는 해당 노드가 어느 구간의 데이터를 포함할지를 뜻합니다. 즉, init(1, 0, 7)의 경우에는 1번 노드가 0번째부터 7번째 배열까지의 데이터를 포함한다는 의미입니다.
이 init 함수는 재귀 함수로 구성되어 start와 end가 같을때, 즉, 구간에 데이터 개수가 1개일때가 종료 조건입니다. 리프 노드가 채워짐과 동시에 다른 노드의 데이터도 채워지게 됩니다.
2.3. 계산
1
2
3
4
5
6
7
8
int sum(int node, int start, int end, int left, int right){
if(left<=start&&end<=right)
return segTree[node];
if(right<start||end<left)
return 0;
int mid = (start + end)/2;
return sum(node*2, start, mid, left, right) + sum(node*2+1, mid+1, end, left, right);
}
입력한 데이터의 left에서부터 right까지의 데이터의 합을 구하는 함수입니다. sum(1, 0, N-1, 0, N-1) 형태로 사용합니다.
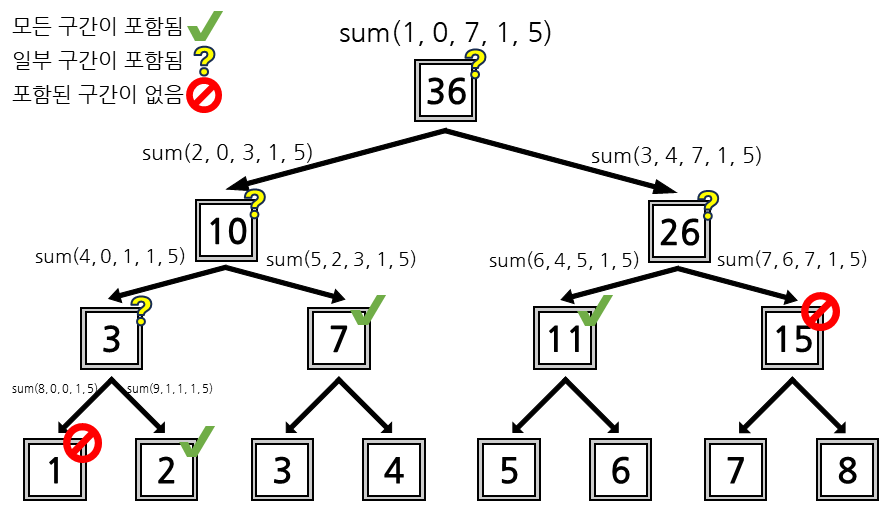
위 함수는 3가지 형태의 반환을 가지고 있습니다.
- 탐색하는 구간이 현재 구간을 모두 포함하는 경우 : 현재 구간에 대한 노드의 값을 반환하니다.
- 탐색하는 구간이 구간을 포함하지 않는 경우 : 0또는 적절한 값을 반환합니다.
- 탐색하는 구간이 일부 구간을 포함하는 경우 : 탐색하는 구간을 절반으로 나눠, 다시 탐색하여 그 값의 합을 반환합니다.
해당 sum함수가 현재 구간을 모두 포함하고 있는 경우 덕에 순회로 리프 노드까지 가지 않아도 되므로, 시간 복잡도가 $O(\log N)$으로 줄어들게 됩니다.
2.4. 갱신
1
2
3
4
5
6
7
8
9
void edit(int node, int start, int end, int index, int diff){
if(start<=index&&index<=end)
segTree[node] -= diff;
else if(start == end)
return;
int mid = (start+end)/2;
edit(node*2, start, mid, index, diff);
edit(node*2+1, mid+1, end, inedx, diff);
}
입력한 데이터의 index번째의 값을 diff만큼 빼는 함수입니다. edit(1, 0, N-1, index, idff) 형태로 사용합니다.
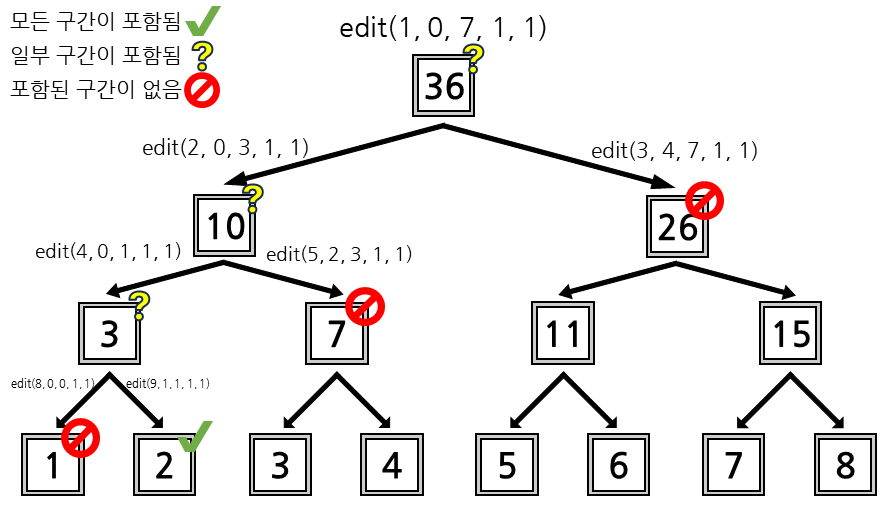
위 함수는 위의 계산 함수와 유사하게 동작합니다.
- index가 현재 구간의 전체인 경우 : 현재 구간의 값을 변경시키고 함수를 종료합니다.
- index가 현재 구간에 포함되지 않는 경우 : 함수를 종료합니다.
- index가 현재 구간에 포함되는 경우 : 현재 구간의 값을 변경시키고 현재 구간을 절반으로 나눠, 각각 구간을 함수 구간으로 하는
edit함수를 실행합니다.
계산 함수와 같이, 모든 리프 노드에 대해서 수정을 하지 않아도 되므로, 데이터 갱신의 경우에도 시간 복잡도 $O(\log N)$으로 해결이 가능합니다.
3. 그래서 이걸 왜?
세그먼트 트리를 점수 복사기가 된 주요한 원인은 세그먼트 트리를 다루는 가장 쉬운 문제인 2042번 구간 합 구하기가 골드 1 문제이기 때문입니다. 즉, 정식 문제 풀이 중에 세그먼트 트리가 포함된다면, 문제의 티어가 모두 골드 1 이상이 된다는 의미입니다.
또한 세그먼트 트리의 모든 함수가 재귀적으로 구성된 것도 한몫 했습니다. 재귀 함수는 코드가 아주 간결해지고 짧아지기 때문에, 코드를 타이핑, 또는 암기하기 쉬운 구조로 되어있습니다.
4. 활용처
다음은 백준에서 세그먼트 트리가 정해 이거나, 세그먼트 트리를 이용하여 해결 할 수 있는 문제들을 서술합니다.
4.1. 구간 합 구하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#define MAX_ARRAY_SIZE 1000001
#define MAX_TREE_SIZE MAX_ARRAY_SIZE * 4
long long segTree[MAX_TREE_SIZE];
long long arr[MAX_ARRAY_SIZE];
long long init(int node, int start, int end){
if(start == end)
return segTree[node] = arr[start];
int mid = (start + end)/2;
return segTree[node] = init(node*2, start, mid) + init(node*2+1 , mid+1, end);
}
long long sum(int node, int start, int end, int left, int right){
if(left<=start&&end<=right)
return segTree[node];
if(right<start||end<left)
return 0;
int mid = (start + end)/2;
return sum(node*2, start, mid, left, right) + sum(node*2+1, mid+1, end, left, right);
}
void edit(int node, int start, int end, int index, long long diff){
if(start<=index&&index<=end)
segTree[node] -= diff;
else if (start == end)
return;
int mid = (start + end)/2;
edit(node*2, start, mid, index, diff);
edit(node*2+1, mid+1, end, index, diff);
}
세그먼트 트리가 활용된 문제중 가장 기본적인 형태인 2042번 구간 합 구하기입니다. 입력 받는 값과 세그먼트 트리에 들어 갈 수 있는 값의 크기가 C언어의 long long와 같으므로 배열과 트리의 자료형을 long long으로 설정했고, 수의 변경 마다 범위에 포함되는 값에 변경되는 차이만큼 빼서 갱신했습니다.
4.2. 최솟값
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#define INF 1000000001
#define MAX_ARRAY_SIZE 100001
#define MAX_TREE_SIZE MAX_ARRAY_SIZE * 4
int segTree[MAX_TREE_SIZE];
int arr[MAX_ARRAY_SIZE];
int MIN(int A, int B){
return A<B?A:B;
}
int init(int node, int start, int end){
if(start == end)
return segTree[node] = arr[start];
int mid = (start + end)/2;
return segTree[node] = MIN(init(node*2, start, mid), init(node*2+1 , mid+1, end));
}
int find(int node, int start, int end, int left, int right){
if(left<=start&&end<=right)
return segTree[node];
if(right<start||end<left)
return INF;
int mid = (start + end)/2;
return MIN(find(node*2, start, mid, left, right), find(node*2+1, mid+1, end, left, right));
}
사칙 연산 대신 두 값을 비교하여 더 작은 값을 세그먼트 트리에 할당하는 10868번 최솟값입니다. 값의 변동은 없으므로 edit 함수는 구현을 하지 않고, MIN함수를 이용하여1 최솟값을 구하는 연산을 진행했습니다.
