C로 배우는 자료구조 (연결 리스트편)
자료 구조는 모든 컴퓨터 관련 학과 학생들이 거쳐가는 관문입니다. 그만큼 자료구조가 아주 중요한 개념 중 하나이며, 이후에 데이터를 처리하는데에 핵심적인 역할을 하게 됩니다.
하지만, 자료구조는 알고리즘과 더불어 뉴비 학살기로 불리는 만큼 난이도가 꽤 있는 편입니다. 왜냐하면 자료구조 강의는 대부분 C로 진행되어, 기초적인 추상 자료형이나 그와 관계된 연산 함수가 기본 라이브러리에 있는 C++, Python과는 다르게 자료형과 함수를 직접 구현해야 하므로 기초 프로그래밍을 배우다가 자료구조로 바로 넘어오는 경우 엄청난 벽을 만나게 됩니다.
그래서 자료구조의 대표적인 자료형인 스택, 큐, 원형 큐, 덱, 연결 리스트, 트리, 그래프를 연결 리스트로 구현하며 정리해보고자 합니다.
1. 연결 리스트
모든 자료형의 기초가 되는 연결 리스트입니다.

연결 리스트의 노드는 대체로 2가지 요소로 만들어 집니다. 저장할 데이터와 다음 노드를 가리키는 포인터입니다.
그리고 연결 리스트 자체를 가리키는 목적으로 사용되는 헤드가 있습니다. 헤드는 대부분 연결 리스트의 가장 첫번째 노드를 가리키고 있으며, 삽입, 삭제 연산에 따라 가리키는 노드가 달라지기도 합니다.
그리고 연결 리스트를 포인터의 개수, 가리키는 위치에 따라 총 3가지로 나눌 수 있습니다. 단순 연결 리스트, 원형 연결 리스트, 이중 연결 리스트입니다.
1.1. 단순 연결 리스트
가장 단순한 단순 연결 리스트입니다. 선 처럼 연결 되어있다 하여 선형 연결 리스트라고도 합니다.
단순 연결 리스트를 이용하여 스택, 큐, 연결 리스트, 그래프를 구현 합니다.
Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* next;
} NODE;
NODE* newLinkedList(){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->next = NULL;
return newNode;
}
void insertFirst(NODE* head, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = head->next;
head->next = newNode;
}
void insertMiddle(NODE* head, int index, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
NODE* ptr = head;
for(int i=0; i<index; i++)
ptr = ptr->next;
newNode->next = ptr->next;
ptr->next = newNode;
}
void insertLast(NODE* head, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = NULL;
for(NODE* ptr=head; ; ptr=ptr->next){
if(!(ptr->next)){
ptr->next = newNode;
break;
}
}
}
void deleteFirst(NODE* head){
NODE* ptr = head->next;
head->next = ptr->next;
free(ptr);
}
void deleteMiddle(NODE* head, int index){
NODE* ptr = head;
for(int i=0; i<index; i++)
ptr = ptr->next;
NODE* removeNode = ptr->next;
ptr->next = removeNode->next;
free(removeNode);
}
void deleteLast(NODE* head){
for(NODE* ptr=head; ; ptr=ptr->next){
if(!((ptr->next)->next)){
free((ptr->next)->next);
ptr->next = NULL;
break;
}
}
}
void traverseNode(NODE* head){
for(NODE* ptr = head->next; ptr; ptr=ptr->next)
printf("%d -> ", ptr->data);
puts("");
}
int main(){
NODE* linkedList;
linkedList = newLinkedList();
insertFirst(linkedList, 4);
insertFirst(linkedList, 2);
insertMiddle(linkedList, 1, 3);
insertLast(linkedList, 5);
insertFirst(linkedList, 1);
traverseNode(linkedList);
deleteFirst(linkedList);
deleteMiddle(linkedList, 2);
deleteLast(linkedList);
traverseNode(linkedList);
}
구현한 연결 리스트의 연산은 가장 앞과 뒤, 그리고 원하는 위치에 값을 삽입하는 insert와 값을 삭제하는 delete, 그리고 노드를 순회하는 traverseNode를 구현했습니다1.
1.2. 원형 연결 리스트
노드가 원형으로 연결되어 순환 할 수 있는 원형 연결 리스트입니다.
원형 연결 리스트를 이용하여 원형 큐를 구현 합니다.
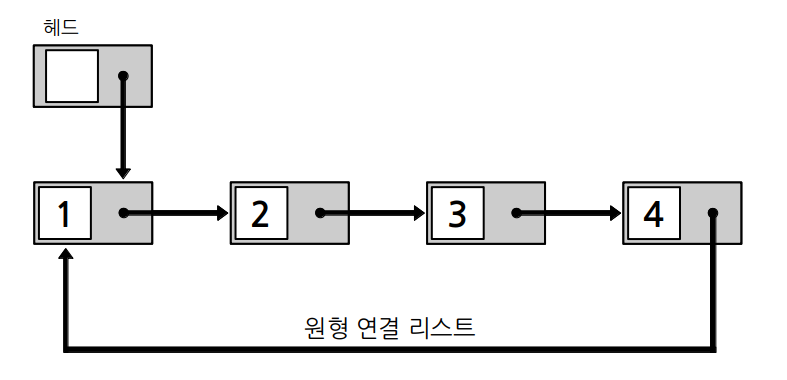
원형 연결 리스트는 삽입, 삭제 연산을 위해서는 가장 앞 노드와 가장 뒤 노드가 필요합니다. 하지만, 가장 뒤 노드를 구하는 연산의 시간 복잡도는 $O(N)$이므로 시간적으로 비효율적입니다.
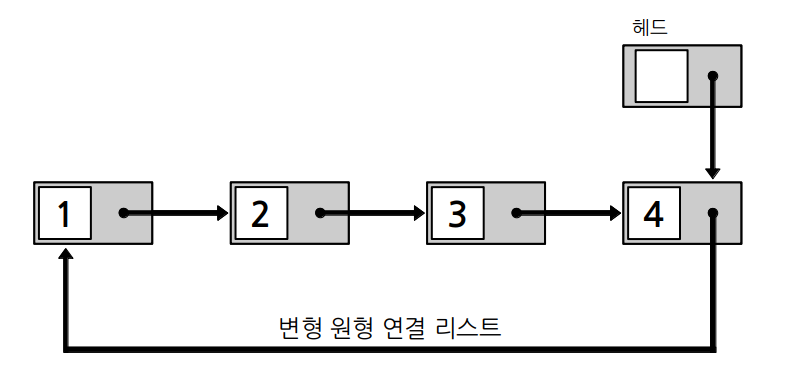
그러므로 변형된 원형 연결 리스트라고도 불리는 방식을 활용합니다. 이는 헤드가 가장 뒤 노드를 가리키는 방식이며, 시간 복잡도 $O(1)$로 가장 앞 노드2와 가장 뒤 노드를 구할 수 있습니다. 이 포스트에서는 변형된 원형 연결 리스트를 구현하겠습니다.
Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* next;
} NODE;
NODE* newLinkedList(){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->next = NULL;
return newNode;
}
void insertFirst(NODE* head, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
if(head->next == NULL){
head->next = newNode;
newNode->next = newNode;
}
else{
newNode->next = ((head->next)->next);
(head->next)->next = newNode;
}
}
void insertMiddle(NODE* head, int index, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
if(head->next == NULL){
head->next = newNode;
newNode->next = newNode;
return;
}
NODE* ptr = head->next;
for(int i=0; i<index; i++)
ptr = ptr->next;
newNode->next = ptr->next;
ptr->next = newNode;
}
void insertLast(NODE* head, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
if(head->next == NULL){
head->next = newNode;
newNode->next = newNode;
}
else{
newNode->next = ((head->next)->next);
(head->next)->next = newNode;
head->next = newNode;
}
}
void deleteFirst(NODE* head){
NODE* ptr = (head->next)->next;
(head->next)->next = ptr->next;
free(ptr);
}
void deleteMiddle(NODE* head, int index){
NODE* ptr = head->next;
for(int i=0; i<index; i++)
ptr = ptr->next;
NODE* removeNode = ptr->next;
if(removeNode == head->next)
head->next = ptr;
ptr->next = removeNode->next;
free(removeNode);
}
void deleteLast(NODE* head){
for(NODE* ptr=(head->next)->next; ; ptr=ptr->next){
if(ptr->next == head->next){
ptr->next = (head->next)->next;
free(head->next);
head->next = ptr;
break;
}
}
}
void traverseNode(NODE* head){
NODE *ptr = (head->next)->next;
do{
printf("%d -> ", ptr->data);
ptr = ptr->next;
}
while(ptr != (head->next)->next);
puts("");
}
int main(){
NODE* linkedList;
linkedList = newLinkedList();
insertFirst(linkedList, 4);
insertFirst(linkedList, 2);
insertMiddle(linkedList, 1, 3);
insertLast(linkedList, 5);
insertFirst(linkedList, 1);
traverseNode(linkedList);
deleteFirst(linkedList);
deleteMiddle(linkedList, 2);
deleteLast(linkedList);
traverseNode(linkedList);
}
이전에 구현한 선형 연결 리스트와는 달리 데이터 삽입시 연결 리스트가 비어있는지 확인 후 비어있다면 자기 자신을 가리키는 노드를 삽입합니다.
또한, 노드를 순회 할때도, 헤드가 가장 뒤 노드를 가리키기에, 가장 앞 노드를 ptr로 지정 하는것을 고려해야 합니다.
1.3. 이중 연결 리스트

노드의 포인터가 두개인 이중 연결 리스트입니다.
이중 연결 리스트를 이용하여 덱을 구현합니다.
Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* next;
struct _NODE* prev;
} NODE;
NODE* newLinkedList(){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->next = NULL;
return newNode;
}
void insertFirst(NODE* head, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = head->next;
newNode->prev = head;
if(head->next)
(head->next)->prev = newNode;
head->next = newNode;
}
void insertMiddle(NODE* head, int index, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
NODE* ptr = head;
for(int i=0; i<index; i++)
ptr = ptr->next;
newNode->next = ptr->next;
newNode->prev = ptr;
if(ptr->next)
(ptr->next)->prev = newNode;
ptr->next = newNode;
}
void insertLast(NODE* head, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = NULL;
for(NODE* ptr=head; ; ptr=ptr->next){
if(ptr->next == NULL){
ptr->next = newNode;
newNode->prev = ptr;
break;
}
}
}
void deleteFirst(NODE* head){
NODE* ptr = head->next;
head->next = ptr->next;
if(ptr->next)
(ptr->next)->prev = head;
free(ptr);
}
void deleteMiddle(NODE* head, int index){
NODE* ptr = head;
for(int i=0; i<index; i++)
ptr = ptr->next;
NODE* removeNode = ptr->next;
ptr->next = removeNode->next;
if(removeNode->next)
(removeNode->next)->prev = ptr;
free(removeNode);
}
void deleteLast(NODE* head){
for(NODE* ptr = head->next; ; ptr=ptr->next){
if(ptr->next == NULL){
(ptr->prev)->next = NULL;
free(ptr);
break;
}
}
}
void traverseNode(NODE* head){
for(NODE* ptr=head->next; ptr; ptr=ptr->next)
printf("%d -> ", ptr->data);
puts("");
}
int main(){
NODE* linkedList;
linkedList = newLinkedList();
insertFirst(linkedList, 4);
insertFirst(linkedList, 2);
insertMiddle(linkedList, 1, 3);
insertLast(linkedList, 5);
insertFirst(linkedList, 1);
traverseNode(linkedList);
deleteFirst(linkedList);
deleteMiddle(linkedList, 2);
deleteLast(linkedList);
traverseNode(linkedList);
}
이중 연결 리스트는 다른 연결 리스트들과는 다르게, 두가지의 포인터를 가지고 있습니다. 그러므로 노드를 삽입, 삭제할때 이전 노드의 포인터도 변경 해야 합니다.
2. 스택
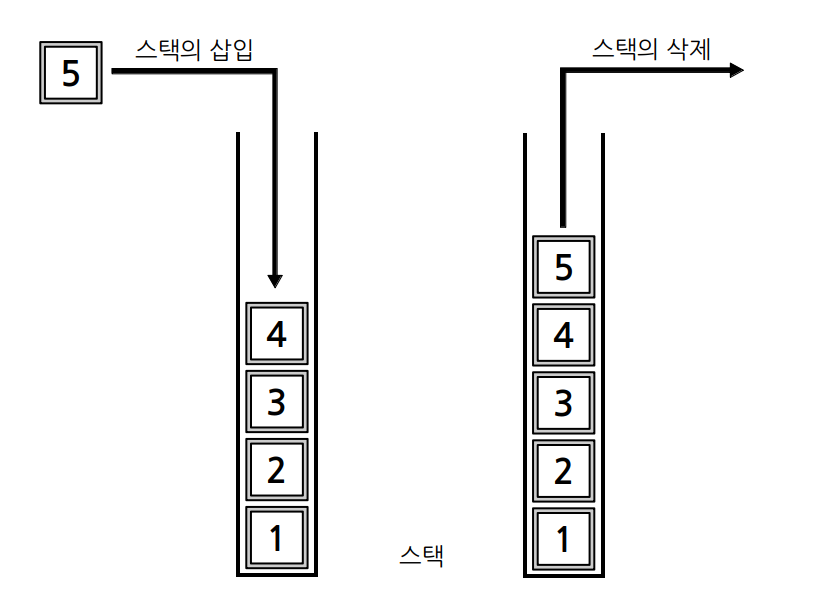
스택(Stack)은 후입선출 구조로 되어있는 자료구조 입니다. 한쪽 끝에서만 자료의 삽입push과 삭제pop가 일어납니다.
2.1. 스택의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _STACK{
NODE* top;
} Stack;
Stack* newStack(){
Stack* S = (Stack *)malloc(sizeof(Stack));
S->top = NULL;
return S;
}
void push(Stack* S, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = S->top;
S->top = newNode;
}
int pop(Stack* S){
NODE* ptr = S->top;
int ret = ptr->data;
S->top = ptr->prev;
free(ptr);
return ret;
}
void traverseStack(Stack* S){
for(NODE* ptr = S->top; ptr; ptr=ptr->prev)
printf("%d -> ", ptr->data);
puts("");
}
int main(){
Stack* S;
S = newStack();
push(S, 1);
push(S, 2);
push(S, 3);
push(S, 4);
push(S, 5);
traverseStack(S);
pop(S);
pop(S);
pop(S);
traverseStack(S);
}
스택은 단순 연결 리스트를 이용하여 구현합니다. 스택은 한 곳에서만 자료의 입력, 출력이 발생하므로, 가장 위 노드(가장 최근에 생성된 노드)인 top을 가리키며 해당 노드를 이용하여 연산합니다.
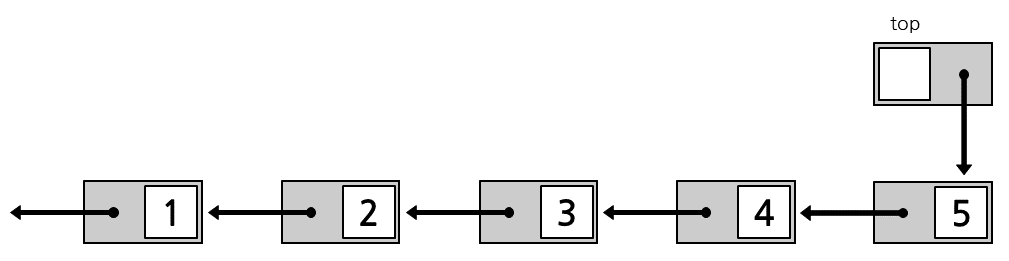
스택이 연결 리스트로 이어져 있는 모습은 다음과 같습니다. top쪽에 있을수록 더 최근에 생성된 노드이고, 각 노드는 자신의 앞 노드(자신보다 먼저 생성된 노드)를 가리켜 삽입, 삭제 연산을 $O(1)$으로 구현합니다3.
2.2. 실습
스택을 직접 활용하기 위해서 백준 10828번 스택을 직접 구현해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _STACK{
NODE* top;
} Stack;
Stack* newStack(){
Stack* S = (Stack *)malloc(sizeof(Stack));
S->top = NULL;
return S;
}
void push(Stack* S, int data){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = S->top;
S->top = newNode;
}
int pop(Stack* S){
NODE* ptr = S->top;
if(ptr == NULL)
return -1;
int ret = ptr->data;
S->top = ptr->prev;
free(ptr);
return ret;
}
int sizeofStack(Stack* S){
int ret = 0;
for(NODE* ptr = S->top; ptr; ptr=ptr->prev)
ret++;
return ret;
}
int main(){
Stack* S;
S = newStack();
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
char input[6];
scanf("%s", input);
switch(input[0]){
case 'p':
if(input[1] == 'u'){ // push
int X;
scanf("%d", &X);
push(S, X);
}
else // pop
printf("%d\n", pop(S));
break;
case 's': // size
printf("%d\n", sizeofStack(S));
break;
case 'e': // empty
printf("%d\n", !(S->top));
break;
case 't': // top
printf("%d\n", S->top?(S->top)->data:-1);
break;
}
}
}
스택이 비었는지는 판별하는 isEmpty 함수는 !(S->top)로 대체 할 수 있습니다. 그리고 스택의 길이를 판별하는 sizeofStack 함수는 기존에 작성했던 traverseStack함수를 재활용하여 작성했습니다. 또한 pop 함수에 에러 핸들링 코드를 추가하여 문제를 풀기위한 코드를 작성했고, 맞았습니다!!
3. 큐
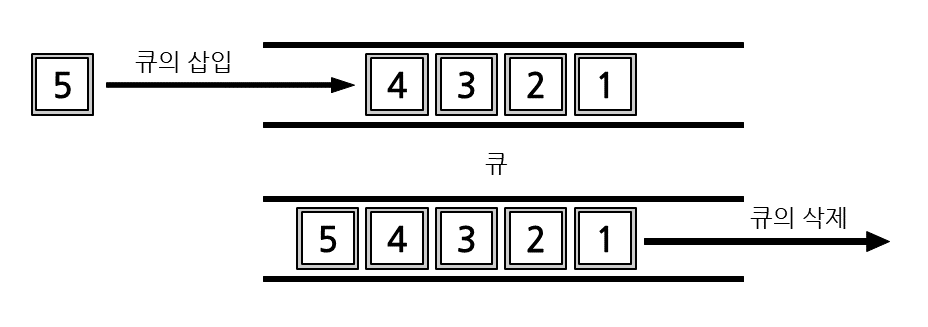
큐(Queue)는 선입선출 구조로 이루어진 자료구조입니다. 한쪽 끝rear에서는 삽입enequeue만 일어나고, 다른쪽 끝front에서는 삭제dequeue만 일어납니다.
3.1. 큐의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _QUEUE{
NODE* rear;
NODE* front;
} Queue;
Queue* newQueue(){
Queue* Q = (Queue*)malloc(sizeof(Queue));
Q->rear = Q->front = NULL;
return Q;
}
void enqueue(Queue* Q, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = NULL;
if(Q->rear)
(Q->rear)->prev = newNode;
else
Q->front = newNode;
Q->rear = newNode;
}
int dequeue(Queue* Q){
NODE* ptr = Q->front;
int ret = ptr->data;
Q->front = ptr->prev;
if(Q->front == NULL)
Q->rear = NULL;
free(ptr);
return ret;
}
void traverseQueue(Queue* Q){
for(NODE* ptr = Q->front; ptr; ptr=ptr->prev)
printf("%d -> ", ptr->data);
puts("");
}
int main(){
Queue* Q;
Q = newQueue();
enqueue(Q, 1);
enqueue(Q, 2);
enqueue(Q, 3);
enqueue(Q, 4);
enqueue(Q, 5);
traverseQueue(Q);
dequeue(Q);
dequeue(Q);
dequeue(Q);
traverseQueue(Q);
}
큐는 단순 연결 리스트를 이용하여 구현합니다. 큐는 스택과 다르게 자료의 입 출력이 다른 방향에서 일어납니다. 그러므로 입력받는 방향인 rear와 출력하는 방향인 front를 이용하여 연산합니다.
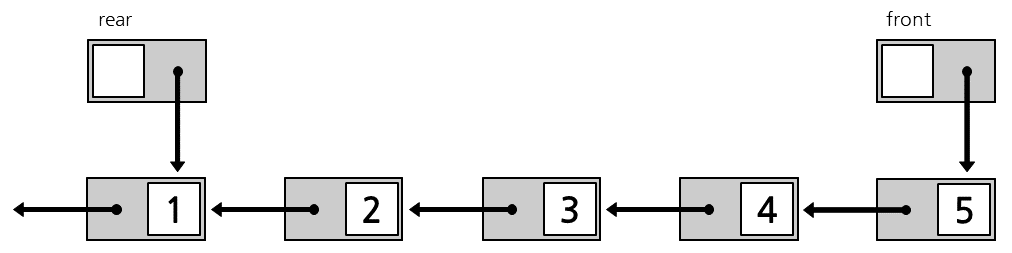
큐 또한 스택과 비슷하게 각 노드가 자신의 앞 노드를 가리킵니다. 이로써 dequeue연산을 할때 시간복잡도 $O(1)$으로 해결할 수 있습니다. 그리고 스택과는 다르게 노드를 가리키는 포인터를 2개 사용하여 연산합니다.
3.2. 실습
백준 10845번 큐를 구현해보면서 실습해 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _QUEUE{
NODE* rear;
NODE* front;
} Queue;
Queue* newQueue(){
Queue* Q = (Queue*)malloc(sizeof(Queue));
Q->rear = Q->front = NULL;
return Q;
}
void enqueue(Queue* Q, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = NULL;
if(Q->rear)
(Q->rear)->prev = newNode;
else
Q->front = newNode;
Q->rear = newNode;
}
int dequeue(Queue* Q){
NODE* ptr = Q->front;
if(ptr == NULL)
return -1;
int ret = ptr->data;
Q->front = ptr->prev;
if(Q->front == NULL)
Q->rear = NULL;
free(ptr);
return ret;
}
int sizeofQueue(Queue* Q){
int ret =0;
for(NODE* ptr = Q->front; ptr; ptr=ptr->prev)
ret++;
return ret;
}
int main(){
Queue* Q;
Q = newQueue();
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
char input[6];
scanf("%s", input);
switch(input[0]){
case 'p':
if(input[1] == 'u'){ // push
int X;
scanf("%d", &X);
enqueue(Q, X);
}
else // pop
printf("%d\n", dequeue(Q));
break;
case 's': // size
printf("%d\n", sizeofQueue(Q));
break;
case 'e': // empty
printf("%d\n", !(Q->front));
break;
case 'f': // front
printf("%d\n", Q->front?(Q->front)->data:-1);
break;
case 'b': // back
printf("%d\n", Q->rear?(Q->rear)->data:-1);
}
}
}
10828번 스택 문제와 유사하게, dequeue의 에러 핸들링과, traverseQueue의 응용으로 sizeofQueue 함수를 제작하여 문제를 맞았습니다!!
4. 원형 큐
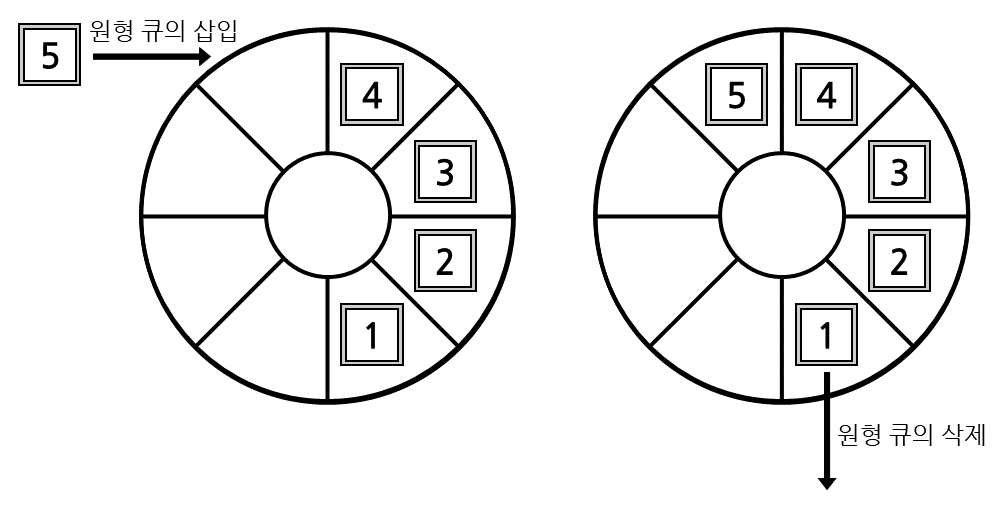
원형 큐(Circular Queue)는 큐와 마찬가지로 선입선출 구조를 가진 자료구조입니다. 하지만 큐와는 다르게 가장 앞 노드와 가장 뒤 노드가 이어져 있어 하나의 포인터로 삽입, 삭제 연산을 할 수 있습니다.
4.1. 원형 큐의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _CQUEUE{
NODE* rear;
} CQueue;
CQueue* newCircularQueue(){
CQueue* CQ = (CQueue*)malloc(sizeof(CQueue));
CQ->rear = NULL;
return CQ;
}
void enqueue(CQueue* CQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
if(CQ->rear){
newNode->prev = (CQ->rear)->prev;
(CQ->rear)->prev = newNode;
}
else
newNode->prev = newNode;
CQ->rear = newNode;
}
int dequeue(CQueue* CQ){
NODE* ptr = (CQ->rear)->prev;
int ret = ptr->data;
if(CQ->rear == ptr)
CQ->rear = NULL;
else
(CQ->rear)->prev = ptr->prev;
free(ptr);
return ret;
}
void traverseCircularQueue(CQueue* CQ){
NODE* rear = (CQ->rear);
for(NODE* ptr = (CQ->rear)->prev; ptr != rear; ptr=ptr->prev)
printf("%d -> ", ptr->data);
printf("%d -> ", rear->data);
puts("");
}
int main(){
CQueue* CQ;
CQ = newCircularQueue();
enqueue(CQ, 1);
enqueue(CQ, 2);
enqueue(CQ, 3);
enqueue(CQ, 4);
enqueue(CQ, 5);
traverseCircularQueue(CQ);
dequeue(CQ);
dequeue(CQ);
dequeue(CQ);
traverseCircularQueue(CQ);
}
원형 큐는 원형 연결 리스트를 이용하여 구현합니다. 원형 연결 리스트의 특성상 제일 끝과 끝이 하나의 정점으로 이어져 있습니다. 그러므로 가장 앞 노드front을 포인터로 지정 할 필요 없이 (CQ->rear)->prev로 사용합니다.
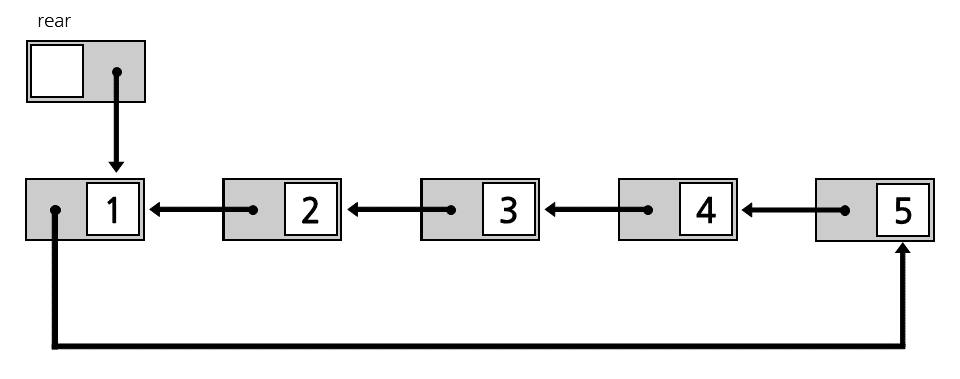
원형 큐는 1.2. 원형 연결 리스트에 설명한 변형 원형 연결 리스트와 원리가 같습니다. 그러므로 front와 rear에 접근하는 시간 복잡도가 $O(1)$이 됩니다. 또한 원형 큐를 순회할때는 먼저 마지막 노드인 rear를 저장하고, rear가 나오기 전까지 노드를 이동하여 순회합니다.
4.2. 실습
백준 1158번 요세푸스 문제를 풀어보며 원형 큐를 실습해 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _CQUEUE{
NODE* rear;
} CQueue;
CQueue* newCircularQueue(){
CQueue* CQ = (CQueue*)malloc(sizeof(CQueue));
CQ->rear = NULL;
return CQ;
}
void enqueue(CQueue* CQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
if(CQ->rear){
newNode->prev = (CQ->rear)->prev;
(CQ->rear)->prev = newNode;
}
else
newNode->prev = newNode;
CQ->rear = newNode;
}
int dequeue(CQueue* CQ){
NODE* ptr = (CQ->rear)->prev;
int ret = ptr->data;
if(CQ->rear == ptr)
CQ->rear = NULL;
else
(CQ->rear)->prev = ptr->prev;
free(ptr);
return ret;
}
void rotateRear(CQueue* CQ){
CQ->rear = (CQ->rear)->prev;
}
int isEmpty(CQueue* CQ){
return !(CQ->rear);
}
int main(){
CQueue* CQ;
CQueue* result;
CQ = newCircularQueue();
result = newCircularQueue();
int N, K;
scanf("%d %d", &N, &K);
for(int i=0; i<N; i++)
enqueue(CQ, i+1);
while(!isEmpty(CQ)){
for(int i=0; i<K-1; i++)
rotateRear(CQ);
enqueue(result, dequeue(CQ));
}
printf("<");
while(!isEmpty(result)){
printf("%d", dequeue(result));
printf("%s", isEmpty(result)?">":", ");
}
}
해당 문제는 원래 큐를 이용하여 구현하는 경우가 많지만, 원형 큐를 이용하여 구현했습니다. 큐로 구현하는 경우는 큐 하나에 대해 $N*K$번 삽입과 삭제 연산을 해야합니다.
하지만 원형 큐를 이용하여 삽입, 삭제를 하지 않고 비교적 가벼운 rotateRear() 함수를 이용하여 rear 포인터를 직접 옮겨 $N$번의 삭제 연산만으로 구현이 가능합니다.
5. 덱
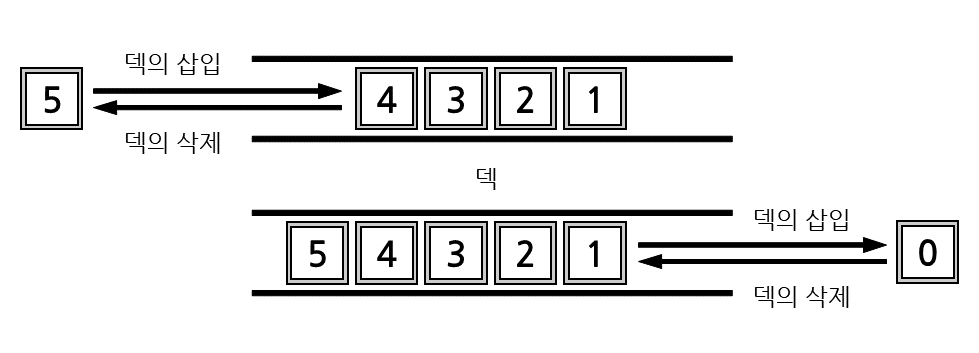
덱(Deque)은 앞으로도, 뒤로도 자료의 삽입과 삭제가 이루어지는 자료구조입니다. Double-ended Queue 라고도 불립니다. 스택과 큐의 특성을 모두 가지고 있습니다.
5.1. 덱의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* next;
struct _NODE* prev;
} NODE;
typedef struct _DEQUE{
NODE* rear;
NODE* front;
} Deque;
Deque* newDeque(){
Deque* DQ = (Deque*)malloc(sizeof(Deque));
DQ->rear = DQ->front = NULL;
return DQ;
}
void addRear(Deque* DQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = DQ->rear;
newNode->prev = NULL;
if(DQ->rear)
(DQ->rear)->prev = newNode;
else
DQ->front = newNode;
DQ->rear = newNode;
}
void addFront(Deque* DQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = DQ->front;
newNode->next = NULL;
if(DQ->front)
(DQ->front)->next = newNode;
else
DQ->rear = newNode;
DQ->front = newNode;
}
int deleteRear(Deque* DQ){
NODE* ptr = DQ->rear;
int ret = ptr->data;
DQ->rear = ptr->next;
free(ptr);
if(DQ->rear)
(DQ->rear)->prev = NULL;
else
DQ->front = NULL;
return ret;
}
int deleteFront(Deque* DQ){
NODE* ptr = DQ->front;
int ret = ptr->data;
DQ->front = ptr->prev;
free(ptr);
if(DQ->front)
(DQ->front)->next = NULL;
else
DQ->rear = NULL;
return ret;
}
void traverseDeque(Deque* DQ){
for(NODE* ptr = DQ->front; ptr; ptr= ptr->prev)
printf("%d -> ", ptr->data);
puts("");
}
int main(){
Deque* DQ;
DQ = newDeque();
addFront(DQ, 3);
addFront(DQ, 2);
addFront(DQ, 1);
addRear(DQ, 4);
addRear(DQ, 5);
traverseDeque(DQ);
deleteFront(DQ);
deleteFront(DQ);
deleteRear(DQ);
traverseDeque(DQ);
}
덱은 이중 연결 리스트를 이용하여 구현합니다. 큐와 같이 제일 앞을 가리키는 포인터와 제일 뒤를 가리키는 포인터를 이용하여 연산합니다.
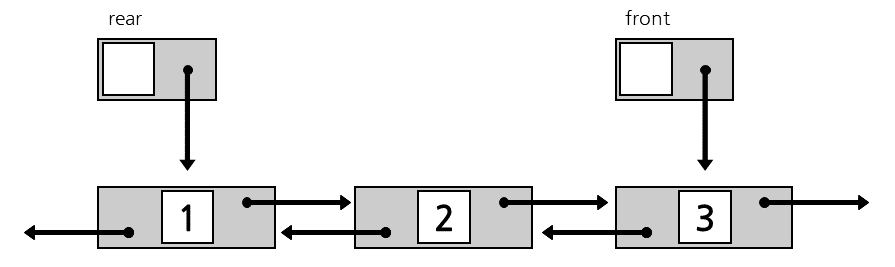
덱은 큐와 유사하게 자료의 삽입과 삭제가 다른 방향에서 이루어지므로, 두개의 포인터가 필요합니다. 해당 포인터를 이용하여 삽입, 삭제 연산에 $O(1)$이 소요됩니다.
5.2. 실습
백준 10866번 덱을 풀어보며 덱을 실습해 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* next;
struct _NODE* prev;
} NODE;
typedef struct _DEQUE{
NODE* rear;
NODE* front;
} Deque;
Deque* newDeque(){
Deque* DQ = (Deque*)malloc(sizeof(Deque));
DQ->rear = DQ->front = NULL;
return DQ;
}
void addRear(Deque* DQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->next = DQ->rear;
newNode->prev = NULL;
if(DQ->rear)
(DQ->rear)->prev = newNode;
else
DQ->front = newNode;
DQ->rear = newNode;
}
void addFront(Deque* DQ, int data){
NODE* newNode = (NODE*)malloc(sizeof(NODE));
newNode->data = data;
newNode->prev = DQ->front;
newNode->next = NULL;
if(DQ->front)
(DQ->front)->next = newNode;
else
DQ->rear = newNode;
DQ->front = newNode;
}
int deleteRear(Deque* DQ){
NODE* ptr = DQ->rear;
if(!ptr)
return -1;
int ret = ptr->data;
DQ->rear = ptr->next;
free(ptr);
if(DQ->rear)
(DQ->rear)->prev = NULL;
else
DQ->front = NULL;
return ret;
}
int deleteFront(Deque* DQ){
NODE* ptr = DQ->front;
if(!ptr)
return -1;
int ret = ptr->data;
DQ->front = ptr->prev;
free(ptr);
if(DQ->front)
(DQ->front)->next = NULL;
else
DQ->rear = NULL;
return ret;
}
int sizeofDeque(Deque* DQ){
int ret = 0;
for(NODE* ptr= DQ->front; ptr; ptr=ptr->prev)
ret++;
return ret;
}
int main(){
Deque* DQ;
DQ = newDeque();
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
char input[11];
int X;
scanf("%s", input);
switch(input[0]){
case 'p':
switch(input[5]){
case 'f': // push_front
scanf("%d", &X);
addFront(DQ, X);
break;
case 'b': // push_back
scanf("%d", &X);
addRear(DQ, X);
break;
case 'r': // pop_front
printf("%d\n", deleteFront(DQ));
break;
case 'a': // pop_back
printf("%d\n", deleteRear(DQ));
break;
}
break;
case 's': // size
printf("%d\n", sizeofDeque(DQ));
break;
case 'e': // empty
printf("%d\n", !(DQ->front));
break;
case 'f': // front
printf("%d\n", DQ->front?(DQ->front)->data:-1);
break;
case 'b': // back
printf("%d\n", DQ->rear?(DQ->rear)->data:-1);
break;
}
}
}
위의 자료구조 구현 문제와 같이, deleteFront, deleteRear의 에러 핸들링과 sizeofDeque의 구현으로 맞았습니다!!
6. 트리
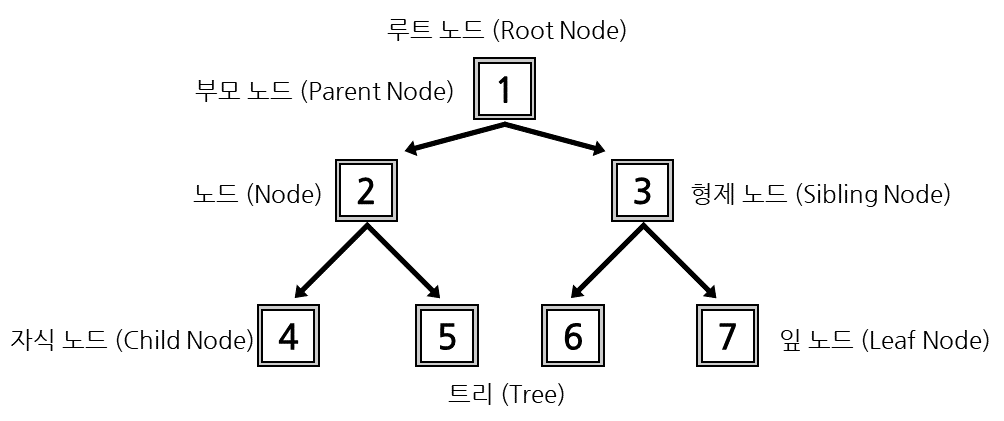
트리(Tree)는 한 노드에서 출발하여 다른 정점들을 순회하여 자기 자신에게 돌아오는 순환이 없는 연결 그래프입니다.
트리는 한 노드가 얼마나 많은 노드를 가리킬수 있는지. 즉 차수(Degree)에 따라 트리와 이진 트리로 나뉘게 됩니다. 트리가 이진트리의 상위 개념입니다.
6.1. 이진 트리
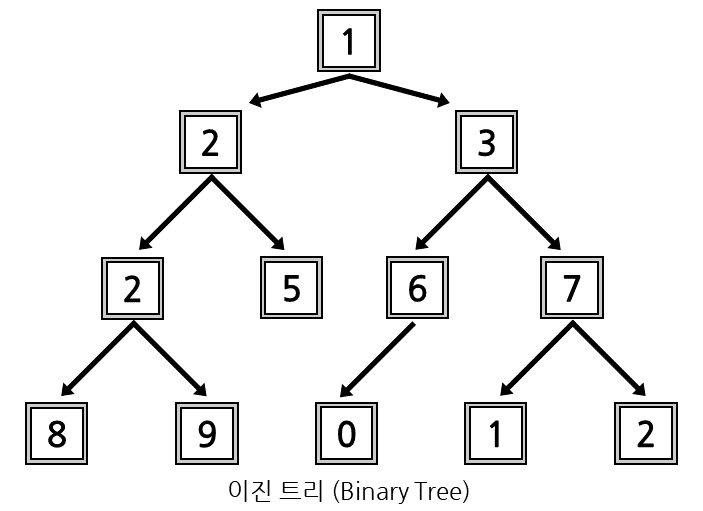
이진트리(Binary Tree)는 트리의 종류중 차수가 2인, 자식 노드의 수가 최대 2인 트리입니다.
6.1.1. 이진 트리의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* left;
struct _NODE* right;
} NODE;
typedef NODE Tree;
NODE* newTree(int data){
NODE* T = (NODE*)malloc(sizeof(NODE));
T->data = data;
T->left = T->right = NULL;
return T;
}
void connectTree(Tree* root, Tree* leftChild, Tree* rightChild){
root->left = leftChild;
root->right= rightChild;
}
void preorder(Tree* root){
if(!root)
return;
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
void inorder(Tree* root){
if(!root)
return;
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
void postorder(Tree* root){
if(!root)
return;
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
int main(){
Tree* root;
Tree* T[12];
for(int i=0; i<12; i++)
T[i] = newTree((i+1)%10);
root = T[0];
connectTree(T[0], T[1], T[2]);
connectTree(T[1], T[3], T[4]);
connectTree(T[2], T[5], T[6]);
connectTree(T[3], T[7], T[8]);
connectTree(T[5], T[9], NULL);
connectTree(T[6], T[10], T[11]);
preorder(root);
puts("");
inorder(root);
puts("");
postorder(root);
}
이진 트리는 이중 연결 리스트로 구현합니다. 트리의 가장 위 노드인 루트(root)노드를 이용하여 트리를 순회합니다.
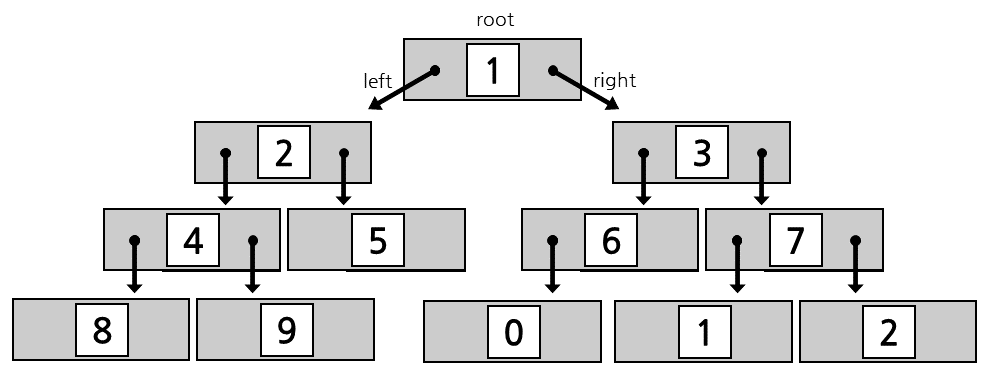
이전의 추상 자료형과는 달리, 트리는 규격화된 삽입, 삭제 연산이 없습니다.4
하지만 노드를 탐색하는 트리 순회는 3가지 종류가 있습니다. 왼쪽 노드로 순회를 L, 현재 노드를 출력하는것을 V, 오른쪽 노드로 순회하는것을 R이라고 할 때, VLR인 전위 순회Preorder Traversal, LVR인 중위 순회Inorder Traversal, LRV인 후위 순회Postorder Traversal로 구성되어있습니다. 이러한 순회들은 재귀 함수로 구현되어 간단하게 표현 가능합니다.
6.1.2. 실습
백준 1991번 트리 순회를 풀어보며 이진 트리를 실습해 봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
char data;
struct _NODE* left;
struct _NODE* right;
} NODE;
typedef NODE Tree;
NODE* newTree(char data){
NODE* T = (NODE*)malloc(sizeof(NODE));
T->data = data;
T->left = T->right = NULL;
return T;
}
void connectTree(Tree* root, Tree* leftChild, Tree* rightChild){
root->left = leftChild;
root->right= rightChild;
}
void preorder(Tree* root){
if(!root)
return;
printf("%c", root->data);
preorder(root->left);
preorder(root->right);
}
void inorder(Tree* root){
if(!root)
return;
inorder(root->left);
printf("%c", root->data);
inorder(root->right);
}
void postorder(Tree* root){
if(!root)
return;
postorder(root->left);
postorder(root->right);
printf("%c", root->data);
}
int main(){
Tree* root;
Tree* T[26];
for(int i=0; i<26; i++)
T[i] = newTree('A'+i);
root = T[0];
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
char L, N, R;
scanf(" %c %c %c", &N, &L, &R);
connectTree(T[N-'A'], L!='.'?T[L-'A']:NULL, R!='.'?T[R-'A']:NULL);
}
preorder(root);
puts("");
inorder(root);
puts("");
postorder(root);
}
우선 트리의 노드를 전부 만들어 둔 뒤, 나중에 입력을 통해 노드들을 각각 잇는것으로 구현했습니다. 또한 이미 구현한 순회들을 이용하여 출력을 하면 맞았습니다!!
6.2. 트리
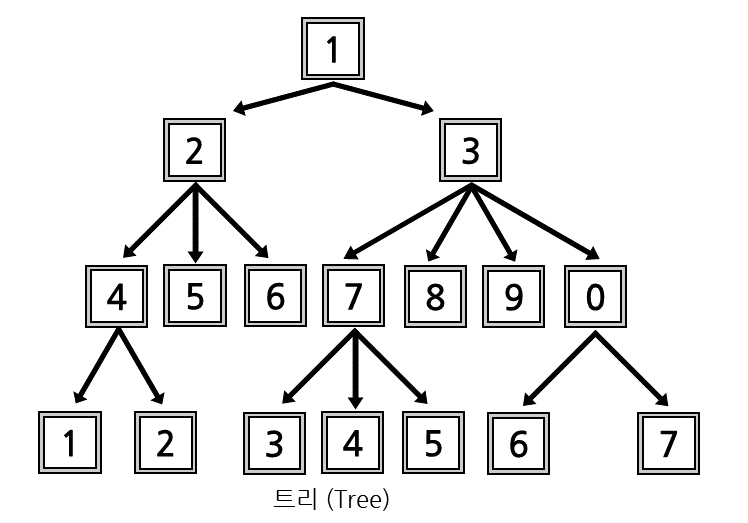
트리(Tree)는 이진 트리를 포함한 순환이 없는 그래프 형태입니다. 이진 트리보다는 활용성, 응용성에서 떨어져 잘 사용하지 않는 자료구조 형태입니다.
6.2.1. 트리의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* child;
struct _NODE* sibilings;
} NODE;
typedef NODE Tree;
NODE* newTree(int data){
NODE* T = (NODE*)malloc(sizeof(NODE));
T->data = data;
T->child = T->sibilings = NULL;
return T;
}
void connectTree(Tree* parent, Tree* child){
if(!parent->child)
parent->child = child;
else{
for(parent = parent->child; parent->sibilings; parent=parent->sibilings);
parent->sibilings = child;
}
}
void traverseTree(Tree* root, int depth){
for(Tree* ptr = root; ptr; ptr=ptr->sibilings){
for(int i=0; i<depth; i++)
printf(" ");
printf("└─%d", ptr->data);
puts("");
if(ptr->child)
traverseTree(ptr->child, depth+1);
}
}
int main(){
Tree* root;
Tree* T[17];
for(int i=0; i<17; i++)
T[i] = newTree((i+1)%10);
root = T[0];
connectTree(T[0], T[1]);
connectTree(T[0], T[2]);
connectTree(T[1], T[3]);
connectTree(T[1], T[4]);
connectTree(T[1], T[5]);
connectTree(T[2], T[6]);
connectTree(T[2], T[7]);
connectTree(T[2], T[8]);
connectTree(T[2], T[9]);
connectTree(T[3], T[10]);
connectTree(T[3], T[11]);
connectTree(T[6], T[12]);
connectTree(T[6], T[13]);
connectTree(T[6], T[14]);
connectTree(T[9], T[15]);
connectTree(T[9], T[16]);
traverseTree(T[0], 0);
}
트리 또한 이진 트리와 같이 이중 연결 리스트를 이용하여 구현합니다. 트리의 가장 위 노드인 루트(root)노드를 이용하여 트리를 순회합니다.
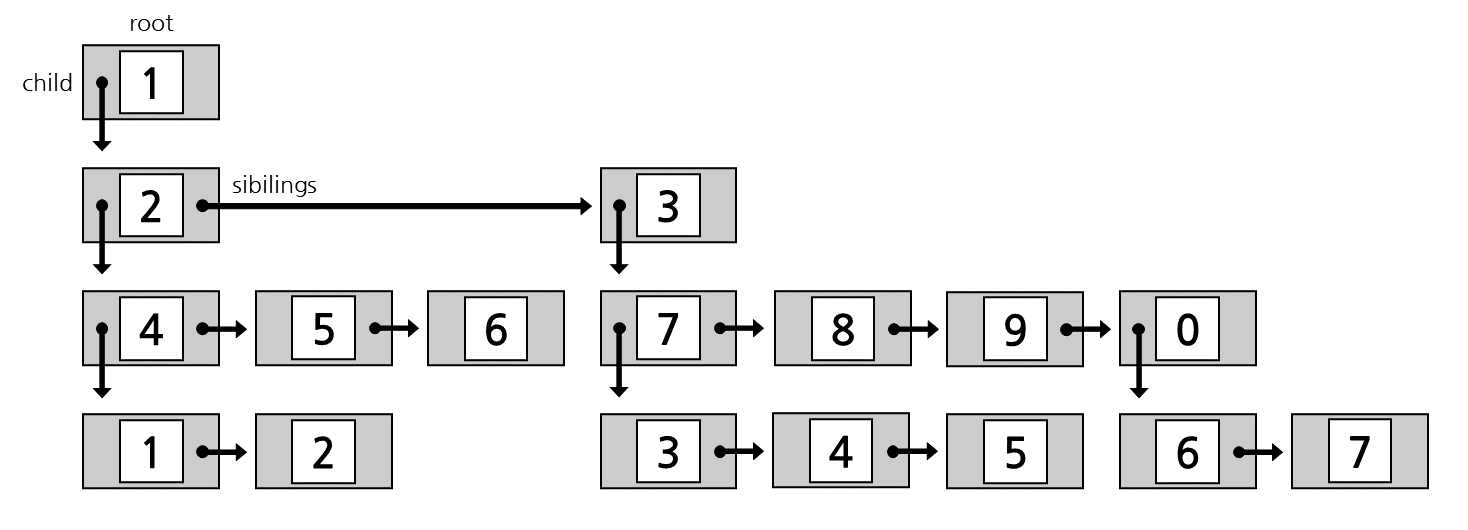
이중 연결 리스트로 구현 할 수 있는 이유는, LCRSLeft Child Right Sibilings 방식을 채택했기 때문입니다.
LCRS는 왼쪽 노드에는 자식 노드Child를 저장하고, 오른쪽 노드에는 형제 노드Sibilings를 저장하는 방식입니다.
예를 들어 7번 노드의 자식 노드는 3번 노드와 4번 노드, 5번 노드입니다. 그러므로 7번 노드의 왼쪽 포인터는 3번 노드를 가리키고, 3번 노드의 오른쪽 포인터는 4번 노드를, 4번 노드의 오른쪽 포인터는 5번 노드를 가리킵니다.
6.2.2. 실습
백준 1068번 트리를 풀어보며 트리를 실습해 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* child;
struct _NODE* sibilings;
} NODE;
typedef NODE Tree;
NODE* newTree(int data){
NODE* T = (NODE*)malloc(sizeof(NODE));
T->data = data;
T->child = T->sibilings = NULL;
return T;
}
void connectTree(Tree* parent, Tree* child){
if(!parent->child)
parent->child = child;
else{
for(parent = parent->child; parent->sibilings; parent=parent->sibilings);
parent->sibilings = child;
}
}
int countLeafNode(Tree* root){
int ret = 0;
if(root->sibilings)
ret += countLeafNode(root->sibilings);
if(root->data == -1)
return ret;
if(root->child){
if(root->child->data != -1 || root->child->sibilings)
ret += countLeafNode(root->child);
else // When a child node is deleted and the parent node has only a deleted child node
ret++;
}
else
ret++;
return ret;
}
int main(){
Tree* root;
Tree* T[50];
for(int i=0; i<50; i++)
T[i] = newTree(i);
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
int parent;
scanf("%d", &parent);
if(parent == -1)
root = T[i];
else
connectTree(T[parent], T[i]);
}
int deleteNode;
scanf("%d", &deleteNode);
T[deleteNode]->data = -1;
printf("%d", countLeafNode(root));
}
이전 1991번 트리 순회와 같이 먼저 트리의 노드를 할당하고, 이후에 부모 자식간의 관계를 입력받아 잇는 방식으로 동작하고, 마지막 리프 노드를 세는 로직에 주의하여 구현하여 맞았습니다!!
7. 그래프
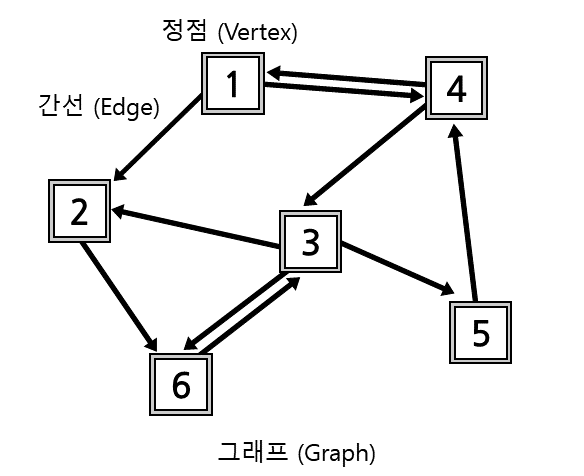
그래프(Graph)는 정점과 간선으로 이루어진 자료 구조입니다. 즉, 그래프는 연결 리스트와 트리를 포함하는 큰 개념입니다.
간선의 특성에 따라 방향을 가지고 있다면 방향 그래프, 가중치가 있다면 가중 그래프로 불립니다.
7.1. 그래프의 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _GRAPH{
NODE* head;
} Graph;
Graph* newGraph(){
Graph* G = (Graph *)malloc(sizeof(Graph));
G->head = NULL;
return G;
}
void addEdge(Graph* G, int vertex){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = vertex;
newNode->prev = G->head;
G->head = newNode;
}
void DFS(Graph* adjList[], int visit[], int start){
visit[start] = 1;
printf("%d ", start);
for(NODE* ptr = adjList[start]->head; ptr; ptr=ptr->prev)
if(!visit[ptr->data])
DFS(adjList, visit, ptr->data);
}
int main(){
Graph* adjList[7];
for(int i=1; i<=6; i++)
adjList[i] = newGraph();
addEdge(adjList[1], 2);
addEdge(adjList[1], 4);
addEdge(adjList[2], 6);
addEdge(adjList[3], 2);
addEdge(adjList[3], 5);
addEdge(adjList[3], 6);
addEdge(adjList[4], 1);
addEdge(adjList[4], 3);
addEdge(adjList[5], 4);
addEdge(adjList[6], 3);
int visit[7] = {0, };
DFS(adjList, visit, 1);
}
그래프는 연결 리스트를 배열에 저장한 인접 리스트(Adjacency List)를 이용하여 구현합니다. 각 연결 리스트는 스택과 형태가 유사하게 동작합니다.

인접 리스트에는 각 노드와 간선으로 연결된 노드의 번호가 연결 리스트로 저장되어 있습니다. 그래프는 여러 순회 방식이 있으며 대표적으로 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)가 있습니다.
7.2. 실습
백준 2606번 바이러스를 풀어보며 실습해 봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>
#include <stdlib.h>
typedef struct _NODE{
int data;
struct _NODE* prev;
} NODE;
typedef struct _GRAPH{
NODE* head;
} Graph;
Graph* newGraph(){
Graph* G = (Graph *)malloc(sizeof(Graph));
G->head = NULL;
return G;
}
void addEdge(Graph* G, int vertex){
NODE* newNode = (NODE *)malloc(sizeof(NODE));
newNode->data = vertex;
newNode->prev = G->head;
G->head = newNode;
}
int DFS(Graph* adjList[], int visit[], int start){
int ret = 1;
visit[start] = 1;
for(NODE* ptr = adjList[start]->head; ptr; ptr=ptr->prev)
if(!visit[ptr->data])
ret += DFS(adjList, visit, ptr->data);
return ret;
}
int main(){
Graph* adjList[101];
for(int i=1; i<=100; i++)
adjList[i] = newGraph();
int V, E;
scanf("%d %d", &V, &E);
for(int i=0; i<E; i++){
int A, B;
scanf("%d %d", &A, &B);
addEdge(adjList[A], B);
addEdge(adjList[B], A);
}
int visit[101] = {0, };
printf("%d", DFS(adjList, visit, 1)-1);
}
노드를 모두 만든 후, addEdge함수로 간선을 만드는 방식으로 그래프를 만들고, DFS로 연결된 정점의 갯수를 새는 방식으로 맞았습니다!!
8. 마치며
7개의 자료구조를 구현 해 보면서 각각의 자료구조의 기초와 활용, 연산법 그리고 연결 리스트의 활용을 알아보았습니다. 해당 내용만 잘 숙지한다면, 자료 구조 과목에서의 이론은 쉽게 이해하리라고 생각합니다.
이후에 C로 배우는 자료구조 (배열편)으로 다시 뵙도록 하겠습니다. 감사합니다.
-
추상 자료형의 연산을 구현하는 중, 에러를 핸들링 하는 코드를 작성하기도 하지만, 이 포스트에서는 동작을 위한 코드만 작성하여 최소화 했습니다. ↩
-
원형으로 연결되어 있어, 가장 뒤 노드의 다음 노드는 가장 앞 노드가 되게 됩니다. ↩
-
만약 노드가 자신의 앞 노드prev가 아닌 뒤 노드next를 가리킨다면 삽입, 삭제 연산에 $O(N)$이 소요됩니다. ↩
-
트리 자체만 놓고 쓰는 경우가 거의 없어 자연스럽게 사용되는 삽입, 삭제 연산이 없는것 같습니다. 트리의 응용형인 힙이나 이진 탑색 트리에는 자체적인 삽입, 삭제 규격이 정해져 있습니다. ↩
